El màxim comú divisor de dos o més nombres és el major divisor natural comú a tots ells.
Si volem calcular el màxim comú divisor de dos o més nombres utilitzant la seua defnició farem el següent:
Començarem escrivint tots els divisors de cada un dels nombres.
Seguidament, assenyalarem tots els divisors que tenen en comú els nombres.
Per a finalitzar prendrem el major d'ells.
Exemple:
Càlcul del màxim comú divisor de 10 y 20. Per a indicar que estem calculant el màxim comú divisor de 10 i 20 ho expressarem de la forma M.C.D.(10 i 20)
Divisors de 10: 1, 2, 5, 10
Divisors de 20: 1, 2, 4, 5, 10 , 20
Els divisors comuns dels nombres són: 1, 2, 5, 10
Per tant, el màxim comú divisor de 10 i 20 és 10 i ho escriurem en la forma M.C.D.(10 i 20)= 10
dimarts, 11 d’abril del 2017
Mínim comú múltiple
El mínim comú múltiple de dos o més nombres és el menor múltiple natural de tots ells.
Si volem calcular el mínim comú múltiple de dos o més nombres utilitzant la seua defnició farem el següent:
Comencem escrivint múltiples de cada un d'ells.
Seguidament, assenyalarem els múltiples comuns a tots ells.
Finalment, prendrem el menor dels múltiples comuns.
Exemple:
Càlcul del mínim comú múltiple dels nombres 2, 6 i 9.Per a indicar que estem calculant el mínim comú múltiple de 2, 6 i 9 ho expressarem de la forma m.c.m.(2, 6 i 9)
Múltiples de 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 48, 50, 52, 54, 56, 58, 60, 62, 64, .....
Múltiples de 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ......
Múltiples de 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, .........
Múltiples comuns: 18, 36, 54
Per tant, el mínim comú múltiple de 2, 6 i 9 és 18 i ho escriurem en la forma m.c.m.(2, 6 i 9)=18
Si volem calcular el mínim comú múltiple de dos o més nombres utilitzant la seua defnició farem el següent:
Comencem escrivint múltiples de cada un d'ells.
Seguidament, assenyalarem els múltiples comuns a tots ells.
Finalment, prendrem el menor dels múltiples comuns.
Exemple:
Càlcul del mínim comú múltiple dels nombres 2, 6 i 9.Per a indicar que estem calculant el mínim comú múltiple de 2, 6 i 9 ho expressarem de la forma m.c.m.(2, 6 i 9)
Múltiples de 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 48, 50, 52, 54, 56, 58, 60, 62, 64, .....
Múltiples de 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ......
Múltiples de 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, .........
Múltiples comuns: 18, 36, 54
Per tant, el mínim comú múltiple de 2, 6 i 9 és 18 i ho escriurem en la forma m.c.m.(2, 6 i 9)=18
Factoritzar un nombre
Factoritzar un nombre és descompondre'l com a producte de nombres primers. Per a això realitzarem successives divisions entre els seus divisors primers fins a obtenir 1 com a quocient.
Per a realitzar les divisions traçarem una barra vertical. A la dreta de la barra escriurem els divisors primers del nombre i a l'esquerra posarem, en primer lloc, el nombre donat i després els successius quocients fins a obtindre l'1..
Açò ho podem veure en l'exemple a continuación

Per a realitzar les divisions traçarem una barra vertical. A la dreta de la barra escriurem els divisors primers del nombre i a l'esquerra posarem, en primer lloc, el nombre donat i després els successius quocients fins a obtindre l'1..
Açò ho podem veure en l'exemple a continuación

Finalmente, escriurem els productes dels factors primers obtinguts. Aquesta expressió la definim com la factoritzación dels nombres.
Obtindre els nombres primers
El coneixement dels nombres primers és important per a calcular la factorització dels nombres i obtindre, a continuació, el màxim comú divisor i el mínim comú múltiple.
Un procediment per a obtindre els nombres primers que hi ha entre els 100 primers nombres naturals es coneix com a la Garbella d'Eratòstenes.
Començarem escrivint tots els nombres naturals des del 2 fins al 100.
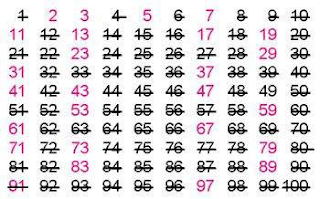
A continuació comptarem de 2 en 2 i ratllarem els nombres corresponents. Després, comptarem de 3 en 3 i ratllarem. I farem el mateix amb els nombres que van quedant, comptant la quantitat que indica cada un d'ells. Aquest procés continuarà fins que no puguem ratllar cap número.
En acabar el procés els números que queden són nombres primers, tal com apareixen a la imatge
Un procediment per a obtindre els nombres primers que hi ha entre els 100 primers nombres naturals es coneix com a la Garbella d'Eratòstenes.
Començarem escrivint tots els nombres naturals des del 2 fins al 100.
A continuació comptarem de 2 en 2 i ratllarem els nombres corresponents. Després, comptarem de 3 en 3 i ratllarem. I farem el mateix amb els nombres que van quedant, comptant la quantitat que indica cada un d'ells. Aquest procés continuarà fins que no puguem ratllar cap número.
Font: https://pinae.wordpress.com/2009/05/19/criba-de-eratostenes/
Font: http://ceper-tavara.blogspot.com.es/2014/10/criba-de-eratostenes.html
diumenge, 9 d’abril del 2017
Càlcul dels divisors d'un nombre
Qualsevol nombre té com a major divisor ell mateix i com a menor divisor l'1. La resta de divisors, si n'hi ha, estàn entre el major i el menor.
Per a calcular tots els divisors d'un nombre seguim el procés següent:
Exemple:
Div (12), representa tots els divisors de 12:
Menor divisor 1, major divisor 12. La resta de divisors, si n'hi ha, els trobarem entre 1 i 12.
12 : 2 = 6 (divisors 2 i 6)
12 : 3 = 4 (divisors 3 i 4)
Escriurem Div (12) : 1, 2, 3, 4, 6, 12
Si es multipliquen els divisors d'un nombre que estàn situats en els extrems, el resultat és el nombre del qual has calculat els seus divisors.
1 . 12, 2 . 6, 3 . 4, el resultat és 12.
Per a calcular tots els divisors d'un nombre seguim el procés següent:
Exemple:
Div (12), representa tots els divisors de 12:
Menor divisor 1, major divisor 12. La resta de divisors, si n'hi ha, els trobarem entre 1 i 12.
12 : 2 = 6 (divisors 2 i 6)
12 : 3 = 4 (divisors 3 i 4)
Escriurem Div (12) : 1, 2, 3, 4, 6, 12
Si es multipliquen els divisors d'un nombre que estàn situats en els extrems, el resultat és el nombre del qual has calculat els seus divisors.
1 . 12, 2 . 6, 3 . 4, el resultat és 12.
dilluns, 27 de març del 2017
Múltiples d'un nombre
Per a aconseguir el múltiple d'un nombre enter qualsevol, hem de multiplicar-ho per qualsevol altre nombre natural.
Exemples de múltiples:
Alguns múltiples dels primers deu nombres enters:
Múltiples d'1: 1, 2, 3, 4, 5,.... 13, ....25,..... 37, .....9875 ...
Múltiples de 2: 2, 4, 6, 8, 10, ....18,.... 26, ....32,... 124,.... 896, ....11112 ...
Múltiples de 3: 3, 6, 9, 12,... 33,... 42,... 69,... 96, ...123,... 231,.... 321, ...456, ....546,.... 564 ...
Múltiples de 4: 4, 8, 12, 16, 20,.... 48,.... 96,.... 132,.... 200,.... 1996,.... 2004 ...
Múltiples de 5: 5, 10, 15, 20,.... 55, ...75,.... 100, ....285,.... 19875 ...
Múltiples de 6: 6, 12, 18, 24, 30,.... 66,.... 192,.... 726,.... 1404,.... 5370 ...
Múltiples de 7: 7, 14, 21, 28, 35....,91,.... 175,.... 364,... 874, ... 3199 ...
Múltiples de 8: 8, 16, 24, 32, 40,.... 72,.... 64,.... 104,... 200,.... 368,.... 441,.... 675, ...1064 ...
Múltiples de 9: 9, 18, 27, 36, 45,.... 81,.... 117,.... 1368 ...
Múltiples de 10: 10, 20, 30, 40, 50,....130,.... 250,.... 440,... 1090, ....2360 ...
Els múltiples d'un nombre són infinits, atès que també són infinits els números naturals.
El menor múltiple d'un nombre es l'1 per a tots el nombres.
Exemples de múltiples:
Alguns múltiples dels primers deu nombres enters:
Múltiples d'1: 1, 2, 3, 4, 5,.... 13, ....25,..... 37, .....9875 ...
Múltiples de 2: 2, 4, 6, 8, 10, ....18,.... 26, ....32,... 124,.... 896, ....11112 ...
Múltiples de 3: 3, 6, 9, 12,... 33,... 42,... 69,... 96, ...123,... 231,.... 321, ...456, ....546,.... 564 ...
Múltiples de 4: 4, 8, 12, 16, 20,.... 48,.... 96,.... 132,.... 200,.... 1996,.... 2004 ...
Múltiples de 5: 5, 10, 15, 20,.... 55, ...75,.... 100, ....285,.... 19875 ...
Múltiples de 6: 6, 12, 18, 24, 30,.... 66,.... 192,.... 726,.... 1404,.... 5370 ...
Múltiples de 7: 7, 14, 21, 28, 35....,91,.... 175,.... 364,... 874, ... 3199 ...
Múltiples de 8: 8, 16, 24, 32, 40,.... 72,.... 64,.... 104,... 200,.... 368,.... 441,.... 675, ...1064 ...
Múltiples de 9: 9, 18, 27, 36, 45,.... 81,.... 117,.... 1368 ...
Múltiples de 10: 10, 20, 30, 40, 50,....130,.... 250,.... 440,... 1090, ....2360 ...
Els múltiples d'un nombre són infinits, atès que també són infinits els números naturals.
El menor múltiple d'un nombre es l'1 per a tots el nombres.
dissabte, 11 de març del 2017
Divisors
Un nombre a és divisor d'un altre nombre b si la divisió de b entre a és exacta.
Si a és divisor de b, llavors b és divisible per a
El nombre de divisors de b és limitat.
Si la divisió de b entre a dòna de quocient c, la divisió de b entre c, dòna de quocient a. Per tant, a i c son divisors de b.
El menor divisor d'un nombre és l'1 i el major és ell mateix.
Exemples:
Divisors de 4: 1, 2, i 4, menor divisor l'1 i major divisor el 4
Divisors de 10 : 1, 2, 5 i 10, menor divisor l'1 i major divisor el 10
Divisors de 15: 1, 3, 5 i 15, menor divisor l'1 i major divisor el 15
Divisors de 36: 1, 2, 3, 4, 9, 12, 18 i 36, menor divisor l'1 i major divisor el 36
Si a és divisor de b, llavors b és divisible per a
El nombre de divisors de b és limitat.
Si la divisió de b entre a dòna de quocient c, la divisió de b entre c, dòna de quocient a. Per tant, a i c son divisors de b.
El menor divisor d'un nombre és l'1 i el major és ell mateix.
Exemples:
Divisors de 4: 1, 2, i 4, menor divisor l'1 i major divisor el 4
Divisors de 10 : 1, 2, 5 i 10, menor divisor l'1 i major divisor el 10
Divisors de 15: 1, 3, 5 i 15, menor divisor l'1 i major divisor el 15
Divisors de 36: 1, 2, 3, 4, 9, 12, 18 i 36, menor divisor l'1 i major divisor el 36
diumenge, 5 de març del 2017
Múltiples d'un nombre: concepte
El concepte de múltiple ho veurem per mitjà d' un exemple:
"El metge m'ha dit que he de pendre'm la pastilla cada quatre hores"
Açò vol dir que me la pendré dins de quatre , huit , dotze, setze, etc.hores. És a dir, repetiré l'acció cada quatre hores. Diem que l'acció de pendre la pastilla es produïx en múltiples de quatre: 4, 8, 12, 16, 20, 24, 28, etc
Açò vol dir que me la pendré dins de quatre , huit , dotze, setze, etc.hores. És a dir, repetiré l'acció cada quatre hores. Diem que l'acció de pendre la pastilla es produïx en múltiples de quatre: 4, 8, 12, 16, 20, 24, 28, etc
Els múltiples d'un nombre s'obtenen multiplicant el nombre pels successius nombres naturals.
.
Quan un nombre és múltiple d'un altre, la divisió del primer entre el segon és exacta, el residu és zero.
Per exemple, 60 és múltiple de 5, perquè la divisió 60:5 és una divisió exacta, quocient 12 i residu zero.
Tots els múltiples d'un nombre són divisibles entre el nombre de forma exacta.
.
Quan un nombre és múltiple d'un altre, la divisió del primer entre el segon és exacta, el residu és zero.
Per exemple, 60 és múltiple de 5, perquè la divisió 60:5 és una divisió exacta, quocient 12 i residu zero.
Tots els múltiples d'un nombre són divisibles entre el nombre de forma exacta.
En l'exemple de la pastilla, tots els nombres, 4,8,12,16, etc són divisibles entre 4.
Propietats dels múltiples:
1. Qualsevol nombre és múltiple de si mateix.
2. Tots els nombres són múltiples de l'1.
3. El producte de dos múltiples d'un nombre és múltiple del nombre.
Propietats dels múltiples:
1. Qualsevol nombre és múltiple de si mateix.
2. Tots els nombres són múltiples de l'1.
3. El producte de dos múltiples d'un nombre és múltiple del nombre.
divendres, 3 de març del 2017
Divisibilitat
Quan la divisió entre dos nombres és exacta diem que existe una relació de divisibilitat entre ells.
És el cas de 45:9, hi ha una relació de divisibilitat entre 45 i 9.
45 és divisible entre 9
Però també podem dir que 45 és múltiple de 9. Si efectuem la divisió exacta tindrem que, per la prova de la divisió, el dividend s'obté multiplicant el divisor pel quocient. En el nostre cas el quocient és 5 i per això, el dividend també és múltiple del quocient.
Finalment, tindrem les següents relacions de divisibilitat en el cas d'una divisió exacta:
Dividend és múltiple del divisor
Dividend és múltiple del quocient
Divisor és divisor del dividend
Quocient és divisor del dividend
En el nostre exemple inicial, podem establir les següents relacions de divisibilitat
45 és múltiple de 9
45 és múltiple de 5
5 és divisor de 45
9 és divisor de 45
És el cas de 45:9, hi ha una relació de divisibilitat entre 45 i 9.
45 és divisible entre 9
Però també podem dir que 45 és múltiple de 9. Si efectuem la divisió exacta tindrem que, per la prova de la divisió, el dividend s'obté multiplicant el divisor pel quocient. En el nostre cas el quocient és 5 i per això, el dividend també és múltiple del quocient.
Finalment, tindrem les següents relacions de divisibilitat en el cas d'una divisió exacta:
Dividend és múltiple del divisor
Dividend és múltiple del quocient
Divisor és divisor del dividend
Quocient és divisor del dividend
En el nostre exemple inicial, podem establir les següents relacions de divisibilitat
45 és múltiple de 9
45 és múltiple de 5
5 és divisor de 45
9 és divisor de 45
dimarts, 28 de febrer del 2017
PLE ( l'entorn d'aprenenatge per l'ensenyament )
PLE ( l'entorn d'aprenenatge per l'ensenyament )
- El suport a l’alumnat per a fixar els seus propis objectius d’aprenentatge.
- Gestionar el seu propi aprenentatge.
- La gestió dels continguts i processos.
- Comunicar-se amb altres en el procés d’aprenentatge.
- Crear i mantindre una xarxa de contactes amb els quals compartir els aprenentatges.
El PLE és l'entorn en el qual aprenem fent servir eficientment les tecnologies. Avui vivim en un món en què la informació s'ha fragmentat i dispersat en múltiples espais per acció de les tecnologies, gairebé qualsevol pot ser creador i proveïdor d'informació i el coneixement avança a velocitats vertiginoses. En aquest context podem definir, conèixer, manejar i enriquir el PLE.
Subscriure's a:
Missatges (Atom)